Das Verfolgungsproblem

„Gehen wir noch vor dem durch oder dahinter?“ fragt Steinchen am Steuer. Der Skipper schaut auf den Frachter, der sich von Steuerbord nähert. „Keinen Stress, Steinchen, seemännische Ruhe und Sicherheit, wir gehen hinter ihm durch. Auch wenn wir Wegerecht haben, wir zeigen deutlich an, dass wir ihn passieren lassen!“ „Also was soll ich machen?“ „Abfallen vom Wind und immer auf sein Heck halten, bis du wieder auf Kurs bist!“ „...immer auf sein Heck halten... ...immer auf sein Heck halten...“ wiederholt Steinchen in Gedanken. Dann kommt die Erleuchtung: “Das ist ja Wahnsinn, ...immer auf sein Heck halten..., wisst ihr was das wird?“ Der Skipper taucht unter Deck ab um der Frage zu entgehen, wir sind oben und müssen durch. „Das ist das klassische Verfolgungsproblem! Männer wir fahren auf einer Verfolgungskurve, das ist glatter Wahnsinn!“ schreit Steinchen und schaut auf unsere Fahrwasserlinie. „Nun krieg` dich mal wieder ein, Steinchen und schau nach vorn, sonst wird das hier noch eine Kavaliershalse!!“ mahnt Dieter. Doch Steinchen ist nicht mehr zu bremsen: „ Das Verfolgungsproblem ist relativ leicht beschrieben, aber mathematisch sehr anspruchsvoll zu lösen. Die erste Erwähnung geht auf den französischen Mathematiker Pierre Bouguer zurück, der das Verfolgungsproblem 1732 so formulierte:

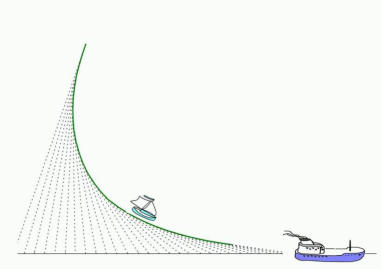
Zwei Schiffe, fahren mit konstanten Geschwindigkeiten auf hoher See;

das eine hält immer Kurs auf das andere, welches sich auf einer Geraden bewegt.

Was für eine Kurve beschreibt das Verfolgerschiff?

Bekannt aber wurde dieses Thema unter dem Namen Hundekurve, der Hund folgt dem vorauslaufenden Herrchen. Übrigens spricht man von einer Traktrix, wenn der Abstand zwischen den Objekten (Hund und Herrchen) gleich bleibt, der Hund also an der Leine ist.) Inzwischen sind viele Varianten des Verfolgungsproblems veröffentlicht, von Katze und Maus, vom Liebhaber zur Angebeteten und vieles andere. Interessante Verfolgungskurven entstehen übrigens auch, wenn sich das Zielobjekt selbst auf einer Kurve (z.B. Kreis oder sinus-Linie) bewegt. Angewandt wird es aber mit einem sehr ernsten Hintergrund, Verfolgungsstrategien im Militärwesen, der Flug- und Raketentechnik. Hier lauten die Aufgabenstellungen: Wie ist der Verfolgungsweg zu wählen, um das Ziel zu treffen, wie sind die Vorhaltewinkel (Schielkurve) zu wählen, welche Reaktionszeiten und Flugeigenschaften können die Vererfolgung garantieren usw. Analog natürlich, wie kann man einem feindlichen Angriff entkommen. Der aufmerksame Segelfreund sollte die Hundekurve übrigens noch aus der Segel-Ausbildung kennen. Hier im Zusammenhang mit der Ansteuerung eines Wegpunktes (homing). Bei Vernachlässigung von Wind- und Stromversatz führt ein sturer rechtweisender Kurs nicht direkt zum Wegziel, sondern man nähert sich auf einer Hundekurve dem Ziel. Der optimale Kurs muss deshalb den Versatz (Wind, Strom, Mißweisung, Ablenkung) direkt berücksichtigen. Formel für die Verfolgungskurve und Ansatz, nach Schirscher

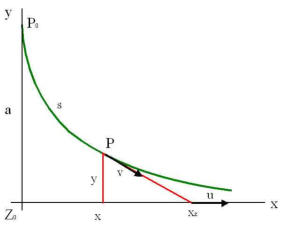
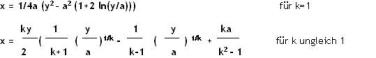
Für alle, die es ganz genau wissen wollen empfehle ich von Prof. G. Schirscher die Veröffentlichung "Verfolgungsprobleme"! Hier sind auch die vollständigen Ableitungen der Formeln nach zu lesen, aber bitte etwas Zeit einplanen, ist nicht ganz trivial! Einfacher in der Praxis: Jeder von uns bewegt sich ständig auf irgendwelchen "Verfolgungskurven" , ob mit dem Fahrrad oder im Auto, immer "schauen" die Hinterräder auf die Vorderräder, die sich auf bestimmten "Fluchtwegen" befinden. Beim Flugzeug (Dreirad) haben die hinteren Räder übrigens noch einen Schielwinkel dabei.

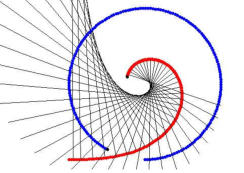
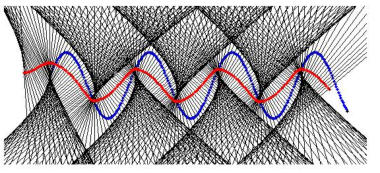
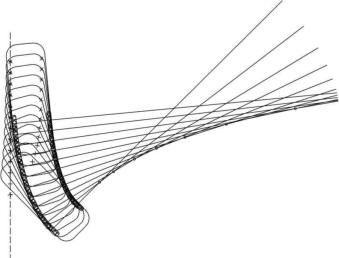
Traktrix beim Ausparken oder Einparken

Im Beispiel fährt ein Auto rückwärts aus einer Parklücke und bewegt sich auf einer Traktrix, das linke Vorderrad wird auf einer Geraden gehalten, um den links daneben parkenden Wagen nicht zu rammen.

Schleppkreis Schlepp-Sinus

s e g e l n - w w w