Was haben Seemannsknoten mit Mathe zu tun?  Sehr viel, wie man gleich sehen kann. Leider aber hilft die Mathematik kaum dabei, Seemannsknoten schneller oder besser zu erlernen. Die Knotentheorie ist ein hochinteressantes Gebiet der Mathematik. Lord Kelvin glaubte, dass Atome Verwirblungen des Äthers seien und begann um 1870, Knoten näher zu untersuchen. Aber dann setzte sich das Atommodell von Niels Bohr durch. Erst im 20. Jahrhundert wurde die Knotentheorie wieder im Zusammenhand mit der Struktur von DNS (Desoxyribonucleinsäure) auf Grund deren molekularen Struktur interessant. Mathematiker sind ordentliche Menschen, also schafften sie zunächst eine "Ordnung”, um Knoten klassifizieren zu können. - der Unknoten ( auch trivialer Knoten) (Knoten werden als unendliche Schleife dargestellt, das hieße für den Segler, immer den Tampen an seinen beiden Ende "zusammen zu schweißen" ) Knoten werden in die Ebene projektiert: Projektion eines Knotens. Zum Beispiel sind die folgenden Knoten nur andere Projektionen des Unknotens:                                                                              der Unknoten oder                                                                                 Trivialknoten                                     Projektionen des Unknotens Eine ganz spezielle Projektion der Unknotensnun ist die einfache Schlinge, was uns nicht wundert, denn wir wissen, dass sich die einfache Schlinge immer mit einem Zug aufziehen lässt. Daher ja auch der Ausdruck, einen Knoten oder ein Seil “auf Slip” legen.

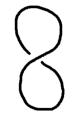
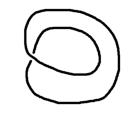
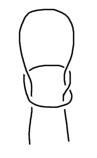
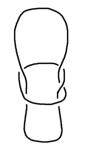
           einfache Schlinge ...                                      ...und die exakte Darstellung                                                                            als Projektion des  trivialen Knotens  

- die Kleeblattschlinge   (wir Seeleute würden sagen:    einfacher  Überhandknoten)   in der mathematischen Nomenklation   wird er geführt als Knoten mit 3 Über-   gängen und der  Conway-Notation:                 (-4) (-1 1 0 1)

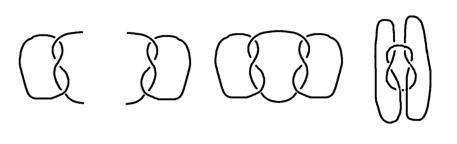
 Interessant wird es für den Seemann, diesen Knoten zweifach zu binden. Genau, es entsteht der bekannte  Kreuzknoten:

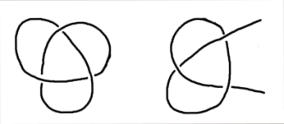
- Primärknoten sind Knoten, die sich nicht auf andere Knoten zurückführen lassen (ausgenommen der Trivialknoten) Nach dieser Definition sind der uns gut bekannten Achterknoten und der Palstek  im mathematischen Sinne Primärknoten! Hier die zugehörigen Abbildungen. Ihr könnt die Knoten an jeder beliebigen Stelle “aufschneiden” - und werdet den Achterknoten bzw. den Palstek erhalten. dieser Knoten hat die mathematische Notation: 4   22 (-2) (1 -1 1 -1 1) und ist ein Primärknoten. In der Seemannsprache bekannt als Achterknoten dieser Knoten hat mathematische Notation: 6  312 (-5)(1 -2 2 -2 2 -1 1) und ist ebenfalls ein Primärknoten. 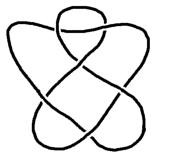In der Seemannsprache bekannt als Palstek dieser Knoten hat mathematische Notation: 7    7 (-10)(-1 1 -1 1 -1 1 0 1) und ist ein Primärknoten. In der Seemannsprache bekannt als Zweifacher oder mehrfacher Überhandknoten (Verdickungsknoten) In  Cillin C. Addams, “Das Knotenbuch”, Einführung in die Knotentheorie oder Dale Berkeley “Knoten und Verschlingungen” sind über 100 primäre Knoten und Verschlingungen dargestellt. Ganz sicher sind darin auch noch weiter Seemannsknoten dabei. Schreibt mir, wenn Ihr was Interessantes findet!  

s e g e l n - w w w