s e g e l n - w w w
Startseite Startseite
Berichte Berichte
Vorbereitung Vorbereitung
Aktuelles Aktuelles
Galerie Galerie
Segeln+Mathematik Segeln+Mathematik
Datenschutz Datenschutz
Kontakt Kontakt
Wie segelt man am Schnellsten von A nach B ?        Diese Frage beherrscht unser oft hektisches Leben. Minuten, ja Sekunden  spielen da oft schon eine Rolle. Aber unterwegs auf dem Wasser bekommt diese Frage eine andere Bedeutung, denn da geht`s um Stunden oder Tage!  Nur 5 Grad neben der optimalen Kurslinie kann bedeuten, dass das Ankerbier erst drei oder fünf Stunden später schmeckt.
An Bord beantwortet jeder diese Frage sofort mit „ VMG –velocity made good“. Das klingt zwar gut, sagt aber noch nichts aus über das Zeitminimum zum Ziel. In der Literatur wird oft die Formel für die „Ziel-Annäherungs-Geschwindigkeit“             VMG = V * cos ß  ,    wobei ß der Winkel zum Ziel ist, herangezogen. Diese Formel beschreibt aber nur den Mehrweg exakt, den das Boot zurücklegen muss. Dabei geht man dann sogar noch davon aus, dass zur Kurskorrektur nach halber Wegstrecke eine Wende oder (Halse) zu fahren ist.            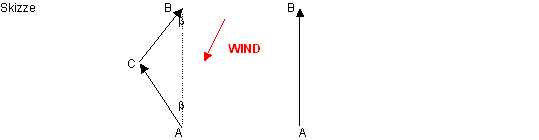Diese Formel unterschlägt nur leider, dass unsere Geschwindigkeit V stark vom Winkel zum Wind a  abhängt. Hinzu kommt noch, dass nach der Wende im Punkt C auf der Strecke CB völlig andere Segelverhältnisse sein werden, als noch AC. In der Skizze bereits ein echtes Problem.
 "Die kürzeste Strecke zwischen zwei Punkte ist die Gerade", sagt die Theorie. Soweit klar, aber  unser Segelboot bewegt sich nach eigenen, windigen Gesetzen. Man kann das Verhältnis von  Windeinfallswinkel zur erreichbaren Geschwindigkeit gut veranschaulichen an Hand der so genannten  Segelkurve, und da wird auch optisch sofort klar, zwischen -315 und 45 Grad geht gar nichts. Die  größten Geschwindigkeiten erreichen moderne Segelyachten mit Halbwind. Natürlich hat jedes Boot seine  eigene Segelkurve, diese wird für mittlere Windstärken angegeben, denn bei höheren Windstärken  ändert sich auch das Segelverhalten (z. B. durch Krängung, Reffs usw).    
Wie ist das Problem also zu lösen ?
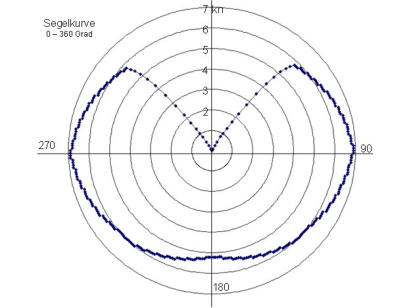
Mit diesem Segelverhalten kann man die zeitoptimale Wegstrecke von A nach B berechnen.
Für unsere Segelkurve erhält man die folgenden Kurslinien, hier für die Einfallwinkel des Windes von 0
bis 45 eingezechnet.
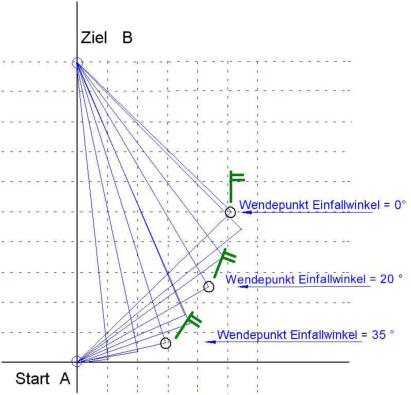
        Wir haben oBdA das Ziel B in Nord gelegt. Aus mathematischer Sicht ist es auch gleichgültig,         ob wir die Fahrt nach Ost oder nach West beginnen, ebenso, ob wir erst auf Höhe fahren und         dann das Ziel ansteuern oder umgekehrt.         Ab dem Einfallswinkel 45 ° liegt das Zeitoptimum fast genau auf der Geraden A nach B, es weicht         nicht mehr als 4 ° ab. Wer Lust hat, sich dieses Thema noch genauer anzusehen, der kann sich mit         relativ einfachen Mitteln ein Programm schreiben.         Ich habe das Ganze mit einer Excel-Tabelle abgebildet.
s e g e l n - w w w