Noch sind es 40 sm bis zum heutigen Tagesziel, das ich spätestens 20 Uhr, also noch vor Einbruch der Dunkelheit erreichen will. Aber der Wind spielt nicht so mit. Es ist jetzt 10 Uhr, aber wir kommen unter Segeln nur mit ca. 3 kn SOG vorwärts. Nur noch 10 Stunden, in denen wir also nur ca. 30 sm unter Segeln schaffen werden. Die Frage also, zu welchem Zeitpunkt muss ich den Motor einschalten, um mit dann ca. 6 kn pünktlich vor Einbruch der Dunkelheit im Hafen zu sein? 1.  Lösung eines Pragmatikers: Du segelst so lange weiter, bis der Quotient aus der Entfernung zum Hafen (in sm) und der verbleibenden Zeit ( in Stunden) gleich 6 ist. Das ist dann genau die Geschwindigkeit 6 kn, die du bis in den Hafen brauchst. 2. 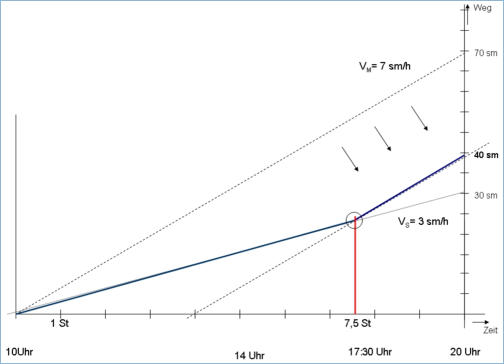Lösung des Ingenieurs: Der Ingenieur löst das Problem graphisch schlicht und einfach mit einem Diagramm. Man sieht, der Motor wird in 7,5 Stunden, also 17:30 Uhr gestartet:

3. Der Mathematiker hat schnell eine Formel zur Hand V S  sei die Geschwindigkeit unter Segeln in der Zeit t S V M  sei die Geschwindigkeit unter Motor in der Zeit t M Z sind die Stunden und    W ist die Entfernung (in sm) bis zum Ziel,  Dann gilt:      V S  * t S  + V M  * t M  =  W      und      t S  + t M  =  Z also V S  * t S  + V M  * ( t S  - Z)  =  W           V M  * Z  - W folgt: t S  =  ------------------                      V M  - V S

In unserem Beispiel:         7 sm/h * 10h  - 40 sm      30 sm t s  =  ------------------------------ =  --------- =   7,5 h      also 17:30 Uhr musst du den Motor  anschalten! 7 sm/h - 3 sm/h        4 sm/h        (wenn du pünktlich zum Anlegebier im Hafen                                                                                 sein willst)

s e g e l n - w w w