Viel früher als gedacht, tauchten die ersten Lichter von Korsika in der Kimm auf. Zuerst glaubten wir, ein weiteres Schiff kreuze unseren Kurs, aber bald war  klar, der Leuchtturm Punta di a Chiappa gab uns sicheres Geleit zur Einfahrt in den Golf von Veccio.  Doch gemach, gemach, noch waren es einige Stunden, bis wir sie erreichen konnten. Schon oft hatte ich diesen Effekt erlebt, dass man die Lichter der nahenden Küste zum Greifen nahe wähnte, aber dann noch Stunden vergingen, ehe man sie erreicht hatte. Was müssen die Seeleute vergangener Tage gespürt haben, wenn sie nach wochen- oder monatelanger Kreuzfahrt endlich die heimatlichen Lichter am Horizont erblickten, die doch noch so weit entfernt leuchteten. Bald konnten wir weitere Lichter an Land erkennen. Kleine Orte vielleicht, Hotels am Strand oder versteckte Fischerhäfen. Es ist sicher schwer, nachts auf eine völlig dunkle Küste zu zufahren, aber es ist auch nicht viel leichter, die Feuer der Hafeneinfahrt an einer von tausenden Lichtern erhellten Küste sicher anzusteuern. Ich habe von erfahrenen Skippern gehört, dass sie bei schwerem Wetter den Yachthafen von Civitaveccio vor Rom nicht angelaufen sind, weil sie durch die Unzahl der Lichter des dahinter liegenden Airports völlig irritiert wurden. Ich selbst bin nachts zwischen der kleinen Insel Formentera und Ibiza hindurchgefahren, im Hintergrund die belebte Stadt Ibiza, den Flughafen und dazwischen irgendwo die befeuerten Seezeichen der Untiefen vor der Küste. Da war größte Wachsamkeit geboten!  "Schätzt doch mal“, fragte der Skipper, „wie weit ist es bis zum Leuchtturm von hier aus?“ Prüfend neigen sich unsere Köpfe im nächtlichen Himmel von backbord nach steuerbord und zurück. Unentschlossen zögernd gaben wir unsere Schätzungen wie Tippscheine beim Buchmacher ab; mancher gleich drei oder vier, die Gewinnchancen erhöhend. Enorm groß dann die Streuung, von 5 bis 20 Seemeilen war so fast alles vertreten. „Ich denke, dass können wir viel genauer bestimmen, auch ohne das GPS zu bemühen. Versucht es doch mal mit der so genannte Kimmformel“, sagte der Skipper, „mit deren Hilfe – so steht es in den schlauen Büchern geschrieben – kann man recht genaue Ergebnisse erzielen. Also:                                                    __        __ Entfernung [in sm] =  2.075 * ( V(t)  +  V(a) )           t ist die Höhe des Lichtes über dem Meer [in m] und a ist die Augenhöhe [in m]. Sofort war Steinchen, unser Mathe-Ass, unter Deck, tauchte aufgeregt mit seinem gelben Heft und der Taschenlampe wieder auf, um sich über die Formel her zu machen. Das war für ihn ja wie eine Erdbeertorte: Eine richtige Formel, mit Summe und Produkt, und als Sahnehäubchen gab es sogar noch zwei Quadratwurzeln dazu. Aber auch zu unserer großen Freude, denn diese Formel sollte uns einige Zeit morgendliche Ruhe und Andacht bescheren. Und das länger als gedacht, denn er saß in seinen Bleistift verbissen und grübelte und grübelte. Hatte Steinchen etwa Probleme mit den Sahnehäubchen? "Wenn du noch lange rechnest, brauchen wir das Ergebnis nicht mehr, denn dann sind wir da!“ drängten wir! Das wurmte Steinchen, er atmete tief durch. „Zum Leuchtturm sind es nach deiner Formel noch genau 19,46  sm. Das ist leicht zu ermitteln. Feuerhöhe des Leuchtturms laut Seekarte              64 m unsere Augenhöhe über Wasser                         ca. 2 m                                      ___       __ Entfernung = 2,075 * (V(64) + V(2)) =   19,46 sm Also etwa noch 20 Seemeilen.“ Anerkennend nickten wir Steinchen zu, der war aber noch nicht zufrieden mit sich und der Welt. „Aber ich habe mir die Formel näher angeschaut und komme noch immer nicht mit dem Faktor 2,075 klar. Bist du dir ganz sicher, Skipper? Nach meinen Rechnungen sollte der Faktor 1,928 lauten.“ „Absolut sicher! 2,075 steht in den Büchern.“ Steinchen beißt sich wieder an seinem Stift fest. „Verstehe ich nicht, sollte größer 2 sein… Habt ihr dazu eine Idee?“, fragt er und zeigt uns in seinem gelben Heft:

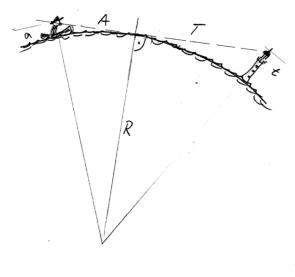
Gesucht ist die Entfernung E = A + T

In der Skizze entstehen zwei rechtwinklige Dreiecke, wenn wir den Betrachter und den Turm zum Erdmittelpunkt verbinden.

Im Punkt W berührt die Blickgerade die Wasseroberfläche (Tangente).

Nun müssen wir wieder einmal die alten Gelehrten bemühen:

I

m rechtwinkligen Dreieck ist die Summe der Katheten-

Quadrate

gleich dem Quadrat ber der Hypotenuse,

sagt der alte Pythagoras.

W

Für unseren Fall heißt das:  T 2  + R 2  = (R + t) 2             und        A 2  + R 2   = (R + a) 2 und ergibt:                        T 2  = R 2  + 2Rt + t 2  – R 2                  A 2  = R 2  + 2Ra + a 2 - R 2                    T 2  = 2Rt + t 2                                 A 2  = 2Ra + a 2 Nun sind wir uns sicher einig, dass bei der Dimension von R (6 378 000 m) die Terms t 2  und a 2  vernachlässigbar sind. Wir können also annehmen T 2  = 2Rt                           und     A 2  = 2Ra Für die Entfernung in Metern erhalten wir jetzt: T + A = QW(2R) * ( QW( t ) + QW ( a ))= QW (2 * 6.378.000) * (Q W( t ) + QW ( a ))= 3571 * ( QW( t ) + QW ( a ) Wir teilen durch 1852  (Umrechnung in Seemeilen) und erhalten E = 1,928 * ( QW( t ) + QW ( a ))    

Aber die Lehrbuchformel enthält den Faktor 2,075.

Steinchen schaut uns traurig an, wir schauen traurig zurück.

Vielleicht hat sich eben dein Pythagoras getäuscht! rief Peter, der die Mathestunde vom Ruder aus verfolgte,

immer mit Blick vorab auf das Leuchtfeuer.

Zu Steinchens Traurigkeit gesellte sich nun auch noch tiefes Mitleid.

„Es gibt wohl keinen Satz der Mathematik, für den man sich mehr Beweise ausgedacht hat, als für den Satz des Pythagoras. Ich glaube es sind über 100! Der für mich schönste ist einfach genial und genial einfach!“ sagt Steinchen und skizziert in das gelbe Ungeheuer:   Aus    (a + b) 2   = 4 * ( ½ ab ) + c 2     folgt    a 2  + 2ab + b 2   = 2ab + c 2              a 2  + b 2  =  c 2

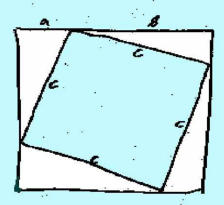
Steinchens Gesicht erstrahlt kurz nach diesem genialen Streich. Doch was ist nun mit dem Faktor in der Kimm- Formel?

Da bist du mit deiner Mathematik am Ende, sagt Peter. Ab hier ist es nämlich reine Physik:

Ich denke, das hängt mit der Ablenkung der Lichtstrahlen in der Atmosphäre zusammen, in der Optik nennt man diesen Effekt Refraktion.

.

Er wirkt besonders, wenn wir die Lichtstrahlen im spitzen Winkel zu den Luftschichten der Atmosphäre wahrnehmen.

Daher sollte er in der Formel nicht vernachlässigt werden. Immerhin kann der Lichtstrahl in Horizontnähe bis zu 0,5° abgelenkt werden,

 das entspricht etwa der scheinbaren Sonnengröße am Himmel.

Wir schauen an einem Sommerabend verträumt in die Sonne. Wenn diese in das Meer eintaucht, dann ist sie aber eigentlich schon gar nicht mehr da.

Du kannst einem ja jede Romantik nehmen! Aber mit der Lichtbrechung hast du Recht. Der Faktor 2,075 berücksichtigt die Refraktion und

damit ist die Kimm-Formel eine gute Näherung für die Entfernung zu einem Feuer in der Kimm. fasste Steinchen befriedigt zusammen.  

Feuer in der Kimm

s e g e l n - w w w